Multi-classification
So you want to predict more than binary classes? Well life is hard and it isn’t as easy. Some approaches
Softmax
For binary classification we would normally take our $z=w^tx $ and calculate the logit $ \frac{1}{1+e^{-z}} $ .
When there are multiple classes there are a few different approaches. First is the softmax
$$ \sigma(z)_j = \frac{e^{z_j}}{\sigma_{k=1}^K e^{z_k}} $$If you have a large number of classes it is computationally expensive to calculate $\sigma(z)_j$ for each class so you can use a hierarchical softmax. For hierarchical softmax there is a binary tree where the input starts at the root and then depending on the response will pick a different path in the tree to find the final label at the roots.
From Ben Wilson’s Building Babylon post on hierarchical softmax the diagram below visualizes this decision tree. This means that instead of having to calculate the class probability for all classes we can calculate output class in log of the number of leaves
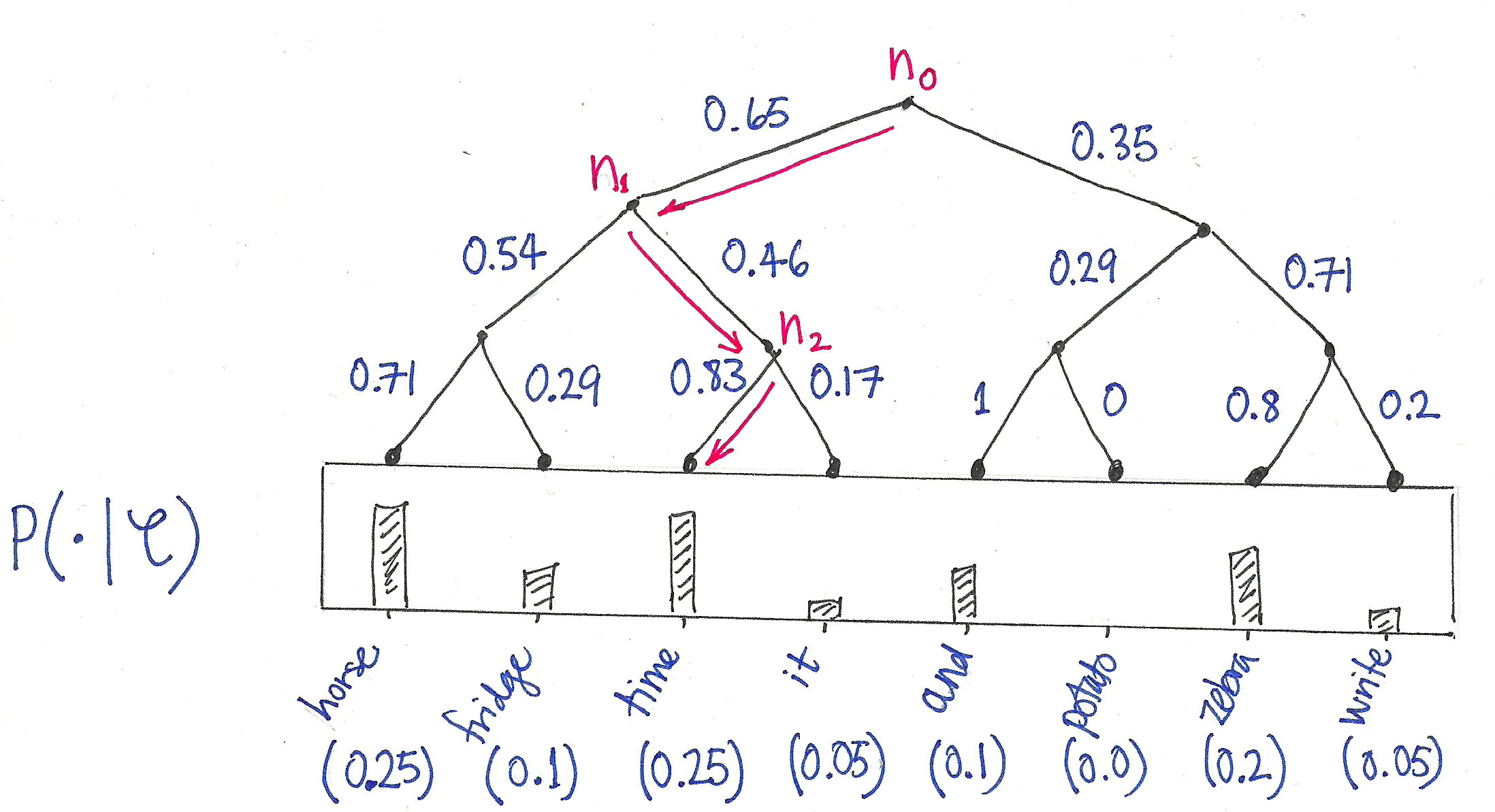
Hierarchical Softmax Tree
Word2vec by Mikolov et al uses a Huffman tree to minimize the expected path from root to leaf and thus the number of parameter updates per training task but then the tree is random from a semantic point of view.
A Scalable Hierarchical Distributed Language Model - Mnih and Hinton, 2008