Factorization Machines
Steven Rendle’s Factorization Machine’s paper is a cool tour de force of showing off a new machine learning approach. He proposes a new model of linear model that can handle very sparse data and automatically model interactions between different variables. Not only is it interesting theoretically but variants have been winners in Kaggle ad CTR prediction contests for Criteo and Avazu and further tried out in real advertising systems at scale and performed well
The core of the model and the idea is that instead of trying to estimate a coefficient for all interactions explicitly we can instead use an embedding of the variable to estimate the interaction between two variables.
$$ \hat{y}(\boldsymbol{x}) := w_0 + \sum_{i=1}^nw_ix_i + \sum_{i=1}^n\sum_{j=i+1}^n\langle v_i,v_j\rangle x_ix_j $$$$ w_0 \in \mathbb{R}, \boldsymbol{w} \in \mathbb{R}, \boldsymbol{V} \in \mathbb{R}^{n\times k} $$This can conveniently be calculated in linear time by rearranging the sums.
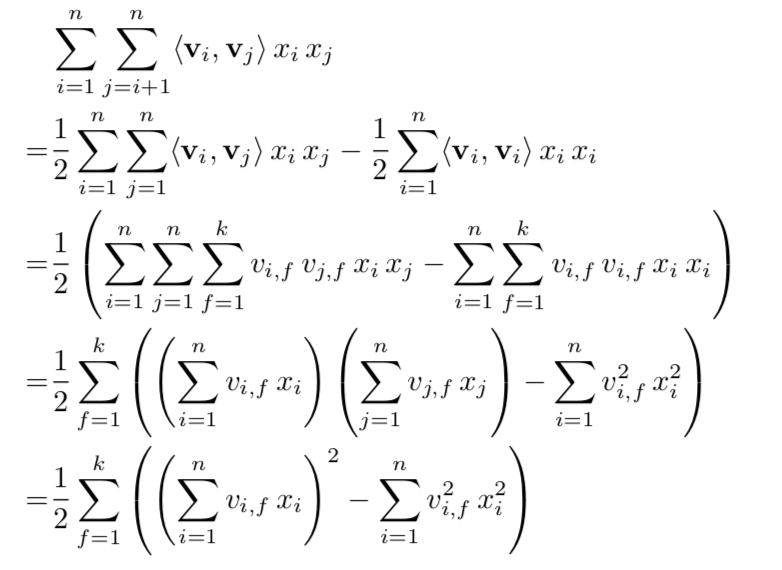
So normally where a regular linear model would have an extra term and $w_i$ coefficient for each interaction here the model has factorized them into an approximation from $\langle v_i,v_j\rangle$, if $K=N$ then all interactions are modeled explicitly but otherwise we are factorizing that $N\times N$ matrix down to $N\times K$.